Physics-Based Simulation

Deformation

We have $\mathbf{X}$ and $\mathbf{x}$ as material coordinates and world coordinates, respectively, each associated with domains ${\Omega }_0$ and ${\Omega }_t$. For any point $\mathbf{X}$ within ${\Omega }_0$, the mapping function $\varphi$ transports it to ${\Omega }_t$ at a specific time $t$, represented as $\mathbf{x}=\varphi (\mathbf{X},t)$.

Definition 12.2.1 (Deformation Gradient). The Jacobian of the deformation map $\varphi$ is referred to as the deformation gradient and is crucial in describing the physics of elasticity. It is commonly denoted as $\mathbf{F}$ and defined by the relation: $$\mathbf{F}(\mathbf{X},t)=\frac{\partial \varphi }{\partial \mathbf{X}}(\mathbf{X},t)=\frac{\partial \mathbf{x}}{\partial \mathbf{X}}(\mathbf{X},t).$$ Discretely, this Jacobian often takes the form of a small $2\times 2$ or $3\times 3$ matrix. For materials like cloth or thin shells in 3D, $\mathbf{F}$ might be a $3\times 2$ matrix, reflecting the 2D nature of the material space. Thus, $\mathbf{F}(\cdot ,t):{\Omega }^0\to {\mathbb{R}}^{d\times d}$ maps every material point $\mathbf{X}$ to a ${\mathbb{R}}^{d\times d}$ matrix that describes the deformation Jacobian at time $t$. Using index notation, it can be expressed as: $$F_{ij}=\frac{\partial {\varphi }_i}{\partial X_j}=\frac{\partial x_i}{\partial X_j},i,j=1,\dots ,d.$$

We can compute the deformation gradient for the deformation map specified in Equation (12.1.1), where the result is the identity matrix. Similarly, for the deformation map in Equation (12.1.2), the deformation gradient $\mathbf{F}$ equals $\mathbf{R}$. In both cases, the object does not undergo real deformation; these are merely examples of rigid transformations. Such deformation gradients should not lead to any internal forces within the material unless artistic effects are intentionally being pursued (such as in a cartoon).

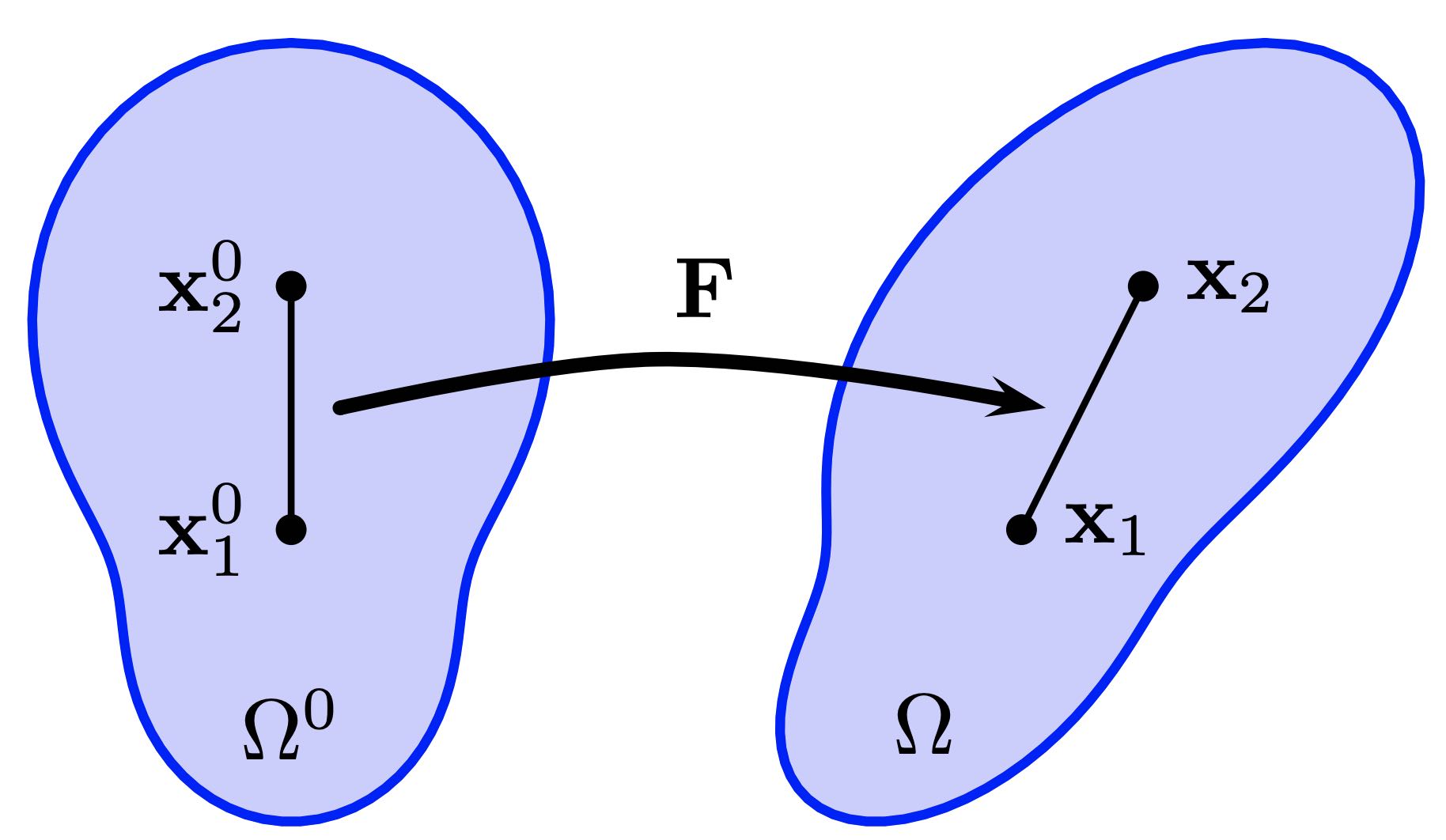
Example 12.2.1. Intuitively, the deformation gradient $\mathbf{F}$ indicates the extent of local deformation within a material. Consider two nearby points, ${\mathbf{x}}_1^0$ and ${\mathbf{x}}_2^0$, embedded in the material at the start of the simulation (as illustrated in Figure 12.2.1). If ${\mathbf{x}}_1$ and ${\mathbf{x}}_2$ represent these points in the current configuration, the relationship between these points can be expressed as: $$({\mathbf{x}}_2-{\mathbf{x}}_1)=\mathbf{F}({\mathbf{x}}_2^0-{\mathbf{x}}_1^0).$$ This equation shows how the deformation gradient transforms the initial distance between the points into their current separation, thus quantifying the local deformation.

The determinant of the deformation gradient $\mathbf{F}$, commonly denoted by $J$, is crucial because it characterizes the infinitesimal volume change during deformation. This is expressed as $J=\det (\mathbf{F})$. The value of $J$ represents the ratio of the infinitesimal volume of the material in the deformed configuration ${\Omega }^t$ to its original volume in ${\Omega }^0$. For instance, in rigid motions, which include rotations and translations, $\mathbf{F}$ is a rotation matrix and therefore $J=1$. Notably, the identity matrix, being a rotation matrix, also results in $J=1$.

If $J>1$, it indicates a volume increase, whereas $J<1$ indicates a decrease. A situation where $J=0$ suggests that the volume has effectively become zero, a scenario that is impossible in the real world but can occur numerically. In 3D, this indicates that the material is compressed to such an extent that it might collapse into a plane, line, or even a point without volume. Conversely, $J<0$ indicates material inversion. For example, in 2D, if $J<0$ for a triangle, it implies that one vertex has passed through the opposing edge, effectively 'inverting' the triangle and making its area negative. As seen in the Moving Boundary Conditions section, severe compression of an elastic square can lead to inversions. In such cases, $J$ serves as a direct measure of this artifact and is utilized in many elasticity models to ensure simulations are free from inversions.