Physics-Based Simulation

Smooth Dynamic-Static Transition

To model frictional contact, local frictional forces $F_k$ can be added for every active contact point pair $k$. For each such pair $k$, at the current state $\{x,v\}$, a consistently oriented sliding basis $T_k(x)\in {\mathbb{R}}^{dm\times d}$ can be constructed, where $m$ is the total number of simulated nodes and $d$ is the dimension of space, such that ${\mathbf{v}}_k=T_k(x{)}^{T}v\in {\mathbb{R}}^d$ provides the local relative sliding velocity that is orthogonal to the distance gradient in the normal direction ${\mathbf{n}}_k(x)$.

Example 9.1.1 (Particle Sliding on Sphere). For a particle with velocity ${\mathbf{v}}_p\in {\mathbb{R}}^3$ moving on the surface of a sphere with velocity ${\mathbf{v}}_s\in {\mathbb{R}}^3$ (no rotation), the relative sliding velocity ${\mathbf{v}}_k$ here can be calculated as $${\mathbf{v}}_k=({\mathbf{v}}_p-{\mathbf{v}}_s)-{\mathbf{n}}_k\cdot ({\mathbf{v}}_p-{\mathbf{v}}_s){\mathbf{n}}_k=({\mathbf{I}}_3-{\mathbf{n}}_k{\mathbf{n}}_k^T)({\mathbf{v}}_p-{\mathbf{v}}_s).$$ If we stack the velocity of the particle and the sphere for this system to obtain $v=[{\mathbf{v}}_p^T,{\mathbf{v}}_s^T{]}^T\in {\mathbb{R}}^6$, we now know that $T_k$ is simply $$T_k(x)=\left[\begin{array}{c}{\mathbf{I}}_3-{\mathbf{n}}_k(x){\mathbf{n}}_k(x{)}^T\\ {\mathbf{n}}_k(x){\mathbf{n}}_k(x{)}^T-{\mathbf{I}}_3\end{array}\right]\in {\mathbb{R}}^{6\times 3}.$$ For more general cases like mesh-mesh contact, the form of $T_k$ only varies in how the relative velocity at the contact point pair $k$ is related to the velocity at the simulated nodes.

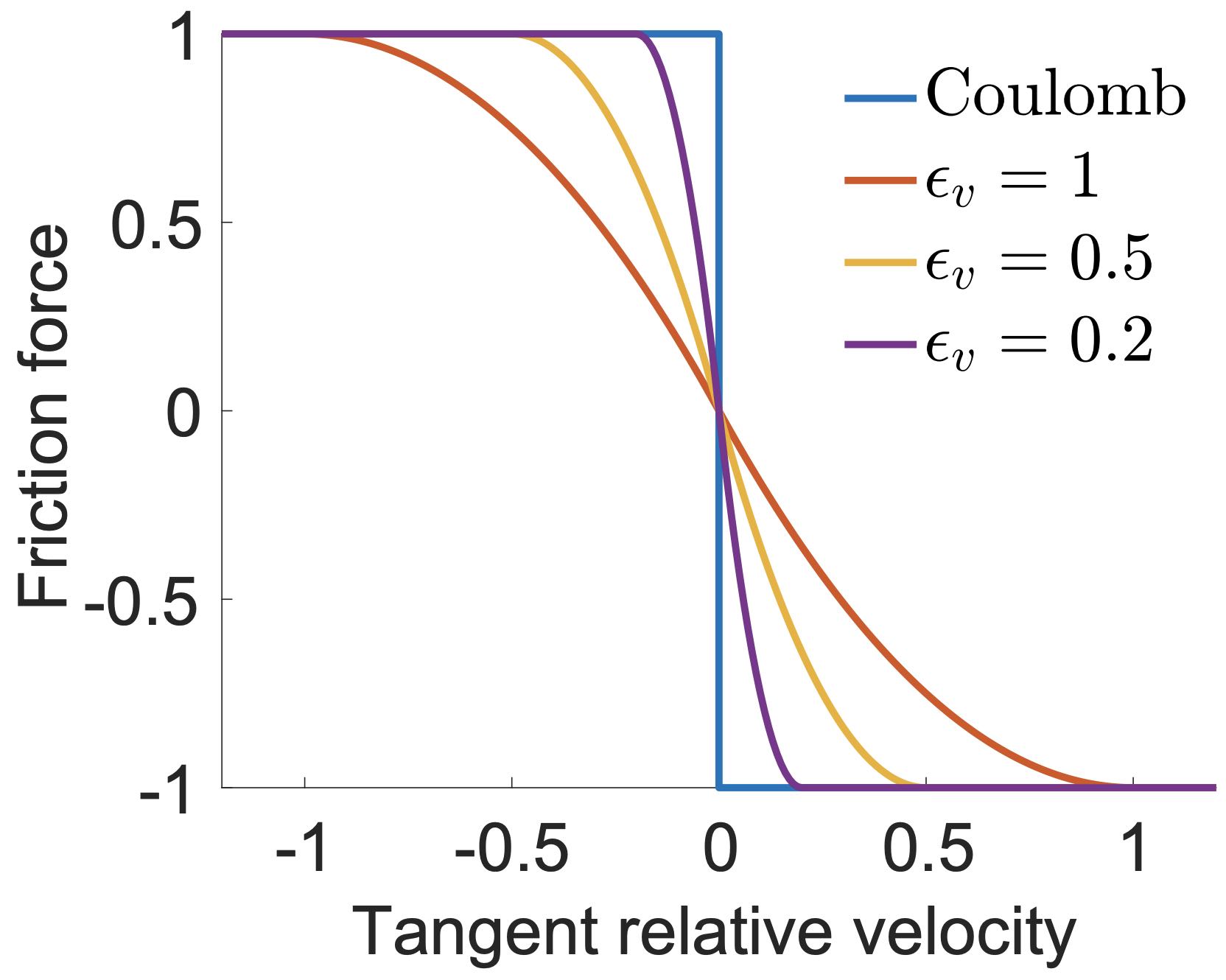
Maximizing dissipation rate subject to the Coulomb constraint defines friction forces variationally $$F_k(x)=T_k(x)\text{arg}\underset{\mathbf{\beta }\in {\mathbb{R}}^d}{\min }{\mathbf{\beta }}^T{\mathbf{v}}_k\text{s.t.}\Vert \mathbf{\beta }\Vert \le \mu {\lambda }_k\text{and}\mathbf{\beta }\cdot {\mathbf{n}}_k=0,\text{\hspace{1em}(9.1.1)}$$ where ${\lambda }_k=-w_k\frac{\partial b}{\partial d_k}$ is the contact force magnitude and $\mu$ is the local friction coefficient. This is equivalent to $$F_k(x)=-\mu {\lambda }_k{T}_k(x)f(\Vert {\mathbf{v}}_k\Vert )\mathbf{s}({\mathbf{v}}_k),\text{\hspace{1em}(9.1.2)}$$ with $\mathbf{s}({\mathbf{v}}_k)=\frac{{\mathbf{v}}_k}{\Vert {\mathbf{v}}_k\Vert }$ when $\Vert {\mathbf{v}}_k\Vert >0$, while $\mathbf{s}({\mathbf{v}}_k)$ takes any unit vector orthogonal to ${\mathbf{n}}_k$ when $\Vert {\mathbf{v}}_k\Vert =0$. In addition, the friction scaling function, $f$, is also nonsmooth with respect to ${\mathbf{v}}_k$ since $f(\Vert {\mathbf{v}}_k\Vert )=1$ when $\Vert {\mathbf{v}}_k\Vert >0$, and $f(\Vert {\mathbf{v}}_k\Vert )\in [0,1]$ when $\Vert {\mathbf{v}}_k\Vert =0$. These non-smoothness would severely slow down and even break convergence of gradient-based optimization.

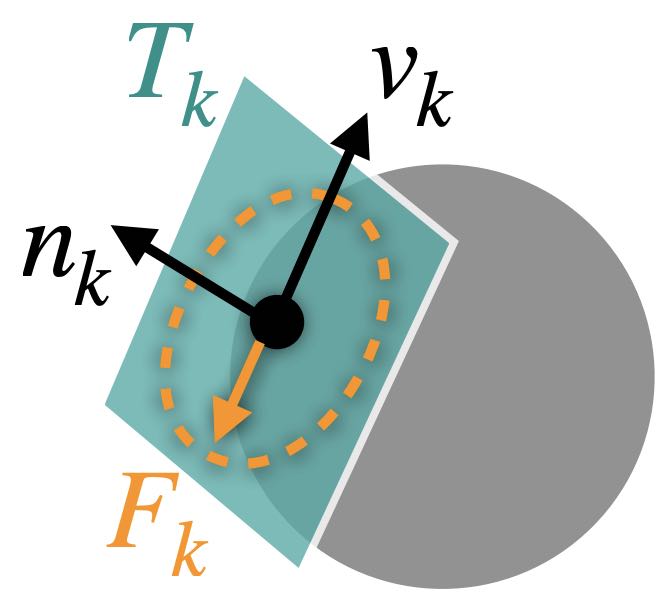
Remark 9.1.1 (Contact Force Magnitude). ${\lambda }_k=-w_k\frac{\partial b}{\partial d_k}$ is the contact force magnitude because at node $k$, the contact force is $-w_k{\nabla }_{{\mathbf{x}}_k}b(d_k(x))=-w_k\frac{\partial b}{\partial d_k}{\nabla }_{{\mathbf{x}}_k}{d}_k(x)$. Therefore, ${\lambda }_k=\Vert -w_k\frac{\partial b}{\partial d_k}{\nabla }_{{\mathbf{x}}_k}{d}_k(x)\Vert =-w_k\frac{\partial b}{\partial d_k}$ since $\frac{\partial b}{\partial d_k}<0$ and $\Vert {\nabla }_{{\mathbf{x}}_k}{d}_k(x)\Vert =1$.

To enable efficient and stable optimization, the friction-velocity relation in the transition to static friction can be mollified by replacing $f$ with a smoothly approximated function. Following IPC, we use $$\begin{array}{r}{f}_1(y)=\{\begin{array}{ll}-\frac{y^2}{{ϵ}_v^2}+\frac{2y}{{ϵ}_v},& y\in [0,{ϵ}_v)\\ 1,& y\ge {ϵ}_v,\end{array}\end{array}\text{\hspace{1em}(9.1.3)}$$ where $f_1^{\prime }({ϵ}_v)=0$ and a velocity magnitude bound ${ϵ}_v$ (in units of $m/s$) below which sliding velocities ${\mathbf{v}}_k$ are treated as static is defined for bounded approximation error (Figure 9.1.2).