Material Particles

In the Material Point Method (MPM), we discretize a solid into a finite set of material points (also referred to as particles), which carry the complete state of the material throughout the simulation. These material points serve as Lagrangian carriers of physical quantities, including:

$x_{p}^{n}$ : the position of particle $p$ (at time $t^{n}$ )
$v_{p}^{n}$ : the velocity of particle $p$
$V_{p}^{n}$ : the volume of particle $p$
$m_{p}$ : the mass of particle $p$ (constant over time)
$F_{p}^{n}$ : the deformation gradient at particle $p$

We adopt the convention that all particle-related quantities are subscripted by $p$ .

Sampling Material Particles

To initialize an MPM simulation, the continuous solid domain is sampled into a finite number of particles. The quality of this sampling has a significant impact on numerical stability and accuracy.

Uniform Grid Sampling. This method places particles at regular intervals on a Cartesian grid. While simple to implement and computationally efficient, it introduces grid-aligned artifacts in simulations, which can reduce realism and robustness.
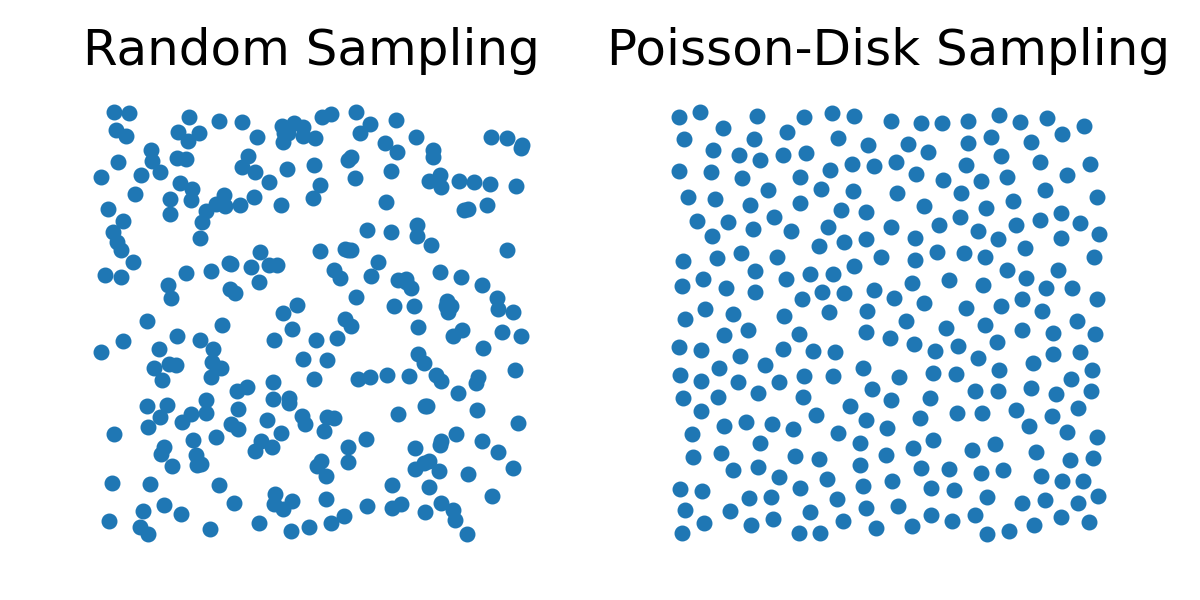
Random Sampling. Naively placing particles at random positions can lead to clustering and large local variations in density, which degrade both simulation accuracy and numerical stability.
Poisson-Disk Sampling. Instead, Poisson-disk Sampling is commonly used because it guarantees a minimum separation between particles, producing a more uniform distribution. This improves interpolation accuracy, minimizes numerical artifacts, and yields more stable contact behavior.

**Figure 27.1.1.** Comparison of random sampling and Poisson-disk sampling in a unit square with the same number of samples: Poisson-disk sampling produces more uniform spacing between points.

Estimating Particle Volume

Since we track the deformation gradient $F_{p}^{n}$ at each particle, we can compute volume change from its determinant: $V_{p}^{n} \approx J_{p}^{n} \cdot V_{p}^{0} = det (F_{p}^{n}) \cdot V_{p}^{0} .$ Here, $V_{p}^{0}$ is the rest volume of particle $p$ , typically computed as: $V_{p}^{0} = \frac{V _{grid_cell}}{N _{particles_per_cell}},$ and we compute $m_{p}$ as: $m_{p} = ρ_{0} \cdot V_{p}^{0},$ where $ρ_{0}$ is the mass density of the solid at rest.