Physics-Based Simulation

Case Study: Hanging Square*

We use a simple case study to end this lecture. Based on the mass-spring system developed in a previous section, we implement gravitational energy and sticky Dirichlet boundary conditions to simulate a hanging square. The excutable Python project for this section can be found at https://github.com/phys-sim-book/solid-sim-tutorial under the 2_dirichlet folder. MUDA GPU implementations can be found at https://github.com/phys-sim-book/solid-sim-tutorial-gpu under the simulators/2_dirichlet folder.

Gravitational energy has $$P(x)=-x^{T}Mg,\nabla P(x)=-Mg,\text{and}{\nabla }^{2}P(x)=0,$$ which can be trivially implemented:

Implementation 5.3.1 (GravityEnergy.py).

import numpy as np

gravity = [0.0, -9.81]

def val(x, m):
    sum = 0.0
    for i in range(0, len(x)):
        sum += -m[i] * x[i].dot(gravity)
    return sum

def grad(x, m):
    g = np.array([gravity] * len(x))
    for i in range(0, len(x)):
        g[i] *= -m[i]
    return g

# Hessian is 0

Then we just need to make sure the gravitational energy is added into the Incremental Potential (IP):

Implementation 5.3.2 (Adding gravity to IP, time_integrator.py).

def IP_val(x, e, x_tilde, m, l2, k, h):
    return InertiaEnergy.val(x, x_tilde, m) + h * h * (MassSpringEnergy.val(x, e, l2, k) + GravityEnergy.val(x, m))     # implicit Euler

def IP_grad(x, e, x_tilde, m, l2, k, h):
    return InertiaEnergy.grad(x, x_tilde, m) + h * h * (MassSpringEnergy.grad(x, e, l2, k) + GravityEnergy.grad(x, m))   # implicit Euler

For the sticky Dirichlet boundary condition, we modify the system accordingly when computing search direction:

Implementation 5.3.3 (DOF elimination, time_integrator.py).

def search_dir(x, e, x_tilde, m, l2, k, is_DBC, h):
    projected_hess = IP_hess(x, e, x_tilde, m, l2, k, h)
    reshaped_grad = IP_grad(x, e, x_tilde, m, l2, k, h).reshape(len(x) * 2, 1)
    # eliminate DOF by modifying gradient and Hessian for DBC:
    for i, j in zip(*projected_hess.nonzero()):
        if is_DBC[int(i / 2)] | is_DBC[int(j / 2)]: 
            projected_hess[i, j] = (i == j)
    for i in range(0, len(x)):
        if is_DBC[i]:
            reshaped_grad[i * 2] = reshaped_grad[i * 2 + 1] = 0.0
    return spsolve(projected_hess, -reshaped_grad).reshape(len(x), 2)

Here is_DBC is an array marking whether a node is Dirichlet or not as we store the Dirichlet node indices in DBC:

Implementation 5.3.4 (DBC definition, simulator.py).

DBC = [n_seg, (n_seg + 1) * (n_seg + 1) - 1]  # fix the left and right top nodes

# ...

# identify whether a node is Dirichlet
is_DBC = [False] * len(x)
for i in DBC:
    is_DBC[i] = True

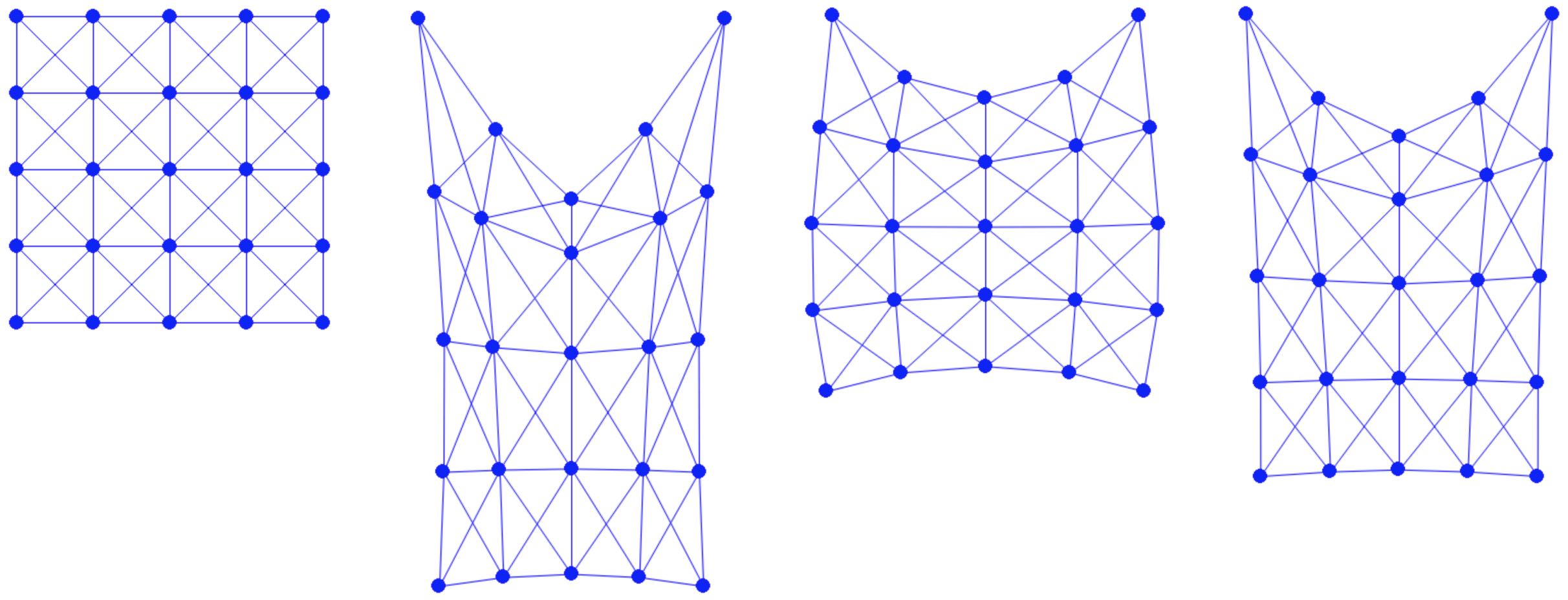
Finally, after making sure is_DBC is passed to the time integrator, we can simulate an energetic hanging square (no initial stretching) with a smaller spring stiffness k=1e3 at framerate time step size h=0.02 (Figure 5.3.1).